7 Hằng đẳng thức đáng nhớ cơ bản và mở rộng

Bảy hằng đẳng thức đáng nhớ là những đẳng thức cơ bản nhất mà mỗi người học toán cần phải nắm vững. Các đẳng thức được chứng minh bằng phép nhân đa thức với đa thức. Những đẳng thức này được sử dụng thường xuyên trong các bài toán liên quan đến giải phương trình, nhân chia các đa thức, biến đổi biểu thức tại cấp học THCS và THPT. Học thuộc 7 hằng đẳng thức đáng nhớ giúp giải nhanh những bài toán phân tích đa thức thành nhân tử.

Trong những hằng đẳng thức này, 1 bên dấu bằng là tổng hoặc hiệu và bên gọi lại là tích hoặc lũy thừa. 7 hằng đẳng thức đáng nhớ được in trong sách giáo khoa bậc THCS ở Việt Nam và được in rất nhiều trong bìa sau của vở viết cấp II hoặc cấp III của học sinh.

Các hằng đẳng thức đáng nhớ

Bình phương của một tổng

Bình phương của một tổng bằng bình phương số thứ nhất cộng với hai lần tích số thứ nhân nhân số thứ hai rồi cộng với bình phương số thứ hai.

(A + B)² = A² + 2AB + B²
 

Bình phương một hiệu

Bình phường của một hiệu bằng bình phương số thứ nhất trừ đi hai lần tích số thứ nhất nhân số thứ 2 rồi cộng với bình phương số thứ hai.

(A - B)² = A² - 2AB + B²

Hiệu hai bình phương

Hiệu hai bình phương bằng hiệu hai số đó nhân tổng hai số đó.

A² – B² = (A + B)(A – B)

Lập phương của một tổng

Lập phương của một tổng = lập phương số thứ nhất + 3 lần tích bình phương số thứ nhất nhân số thứ hai + 3 lần tích số thứ nhất nhân bình phương số thứ hai + lập phương số thứ hai.

(A + B)³ = A³ + 3A²B + 3AB² + B³

Lập phương của một hiệu

Lập phương của một hiệu = lập phương số thứ nhất - 3 lần tích bình phương số thứ nhất nhân số thứ hai + 3 lần tích số thứ nhất nhân bình phương số thứ hai - lập phương số thứ hai.

(A - B)³ = A³ - 3A²B + 3AB² - B³

Tổng hai lập phương

Tổng của hai lập phương bằng tổng hai số đó nhân với bình phương thiếu của hiệu.

A³ + B³  = (A + B)(A² – AB + B²)

Hiệu hai lập phương

Hiệu của hai lập phương bằng hiệu của hai số đó nhân với bình phương thiếu của tổng.

A³ – B³ = (A – B)(A² + AB + B²)

Các hệ thức liên quan

• (a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc
• (a + b - c)² = a² + b² + c² + 2ab - 2ac - 2bc
• (a - b - c)² = a² + b² + c² - 2ab - 2ac + 2bc
• (a + b + c)³ = a³ + b³ + c³ + 3(a + b)(b + c)(a + c)
• a³ + b³ + c³ - 3abc = (a + b + c)(a² + b² + c² - ab - bc - ac)

Các dạng bài tập lưu ý

Bài 16 trang 11 sách giáo khoa Toán lớp 8

Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu;

a) 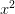 + 2x + 1;                b) 9 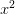+  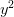+ 6xy;

c) 25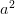 + 4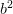 – 20ab;       d)  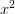– x + 14

Giải:

a)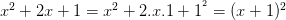 

b)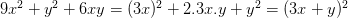 

c)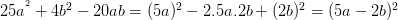 

d)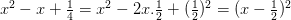 

 

Bài 17 trang 11 sách giáo khoa Toán lớp 8

Chứng minh rằng:

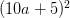 = 100a . (a + 1) + 25.

Từ đó em hãy nêu cách tính nhẩm bình phương của một số tự nhiên có tận cùng bằng chữ số 5.

Áp dụng để tính:  ,   ,  , .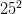

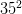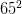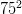Nhận xét:

Cách tính nhẩm bình phương của một số có tận cùng bằng chữ số 5 thì bằng 100 lần chữ sô hàng chục nhân với số hàng chục cộng 1 rồi lấy kết quả cộng với 25.

Giải:

Biến đồi vế trái ta có:

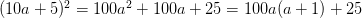
Cách tính nhẩm bình phương của một sô có tận cùng bằng chữ sô 5 thì bằng 100 lần chữ số hàng chục nhân với sô hàng chục

cộng 1 rồi lấy kết quả cộng với 25.

Áp dụng: 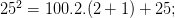 = 200.3 + 25 = 600 + 25 = 625

Tương tự ta có: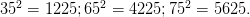 

Ngoài ra, ta có thể tính nhẩm bình phương của một sô có tận cùng bằng chữ số 5.

• Lấy số tận cùng bình phương được 25, giữ nguyên.
• Lấy số hảng chục cộng 1 nhân với chính nó, được bao nhiêu ghi liền trước sô 25 ta được kết quả.

Áp dụng: 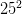= 625;…