Định lý Talet trong tam giác, trong hình thang – Toán lớp 8
Danh mục nội dung
Tỉ số của hai đoạn thẳng
Tỉ số của hai đoạn thẳng là gì? Tỉ số của 2 đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Tỉ số của hai đoạn thẳng AB và CD được kí hiệu là AB/CD
Chú ý: Tỉ số của hai đoạn thẳng không phụ thuộc vào các chọn đơn vị đo.
Đoạn thẳng tỉ lệ
Giả sử ta có 2 đoạn thẳng AB và CD. Hai đoạn thẳng này gọi là tỷ lệ với 2 đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức:
AB/CD = A’B’/C’D’ hay AB/A’B’ = CD/C’D’
Định lý Talet trong tam giác
Định lý Talet thuận
Nếu có một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ xuất hiện những cặp đoạn thẳng tỉ lệ trên hai cạnh bị cắt đó.
Ta có tam giác ABC, đường thẳng d cắt AB tại D, cắt AC tại E và d song song với BC.
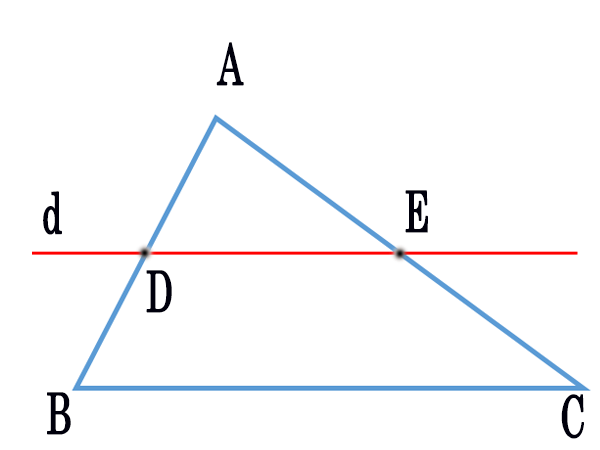
Theo định lý Talet ta được:
AD/AB = AE/AC hay AD/DB = AE/EC hay DB/AB = EC/AC
Định lý talet đảo
Khi xuất hiện một cặp cạnh tỉ lệ trên hai cạnh của một tam giác thì sẽ xuất hiện trên hai cạnh đó một đường thẳng song song với cạnh còn lại của tam giác.
Lưu ý: Định lý vẫn đúng cho trường hợp đường thẳng cắt phần kéo dài hai cạnh của tam giác.
Với hình minh họa trên, tam giác ABC có AD/AB = AE/AC hay AD/DB = AE/EC hay DB/AB = EC/AC
Theo định lý Talet đảo ta được: DE song song với cạnh BC (Ký hiệu: DE//BC)
Hệ quả
Hệ quả 1: Một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới có 3 cạnh tỉ lệ với 3 cạnh của tam giác ban đầu.
Hệ quả 2: Một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới đồng dạng với tam giác ban đầu.
Hệ quả 3 - Talet mở rộng: Ba đường thẳng đồng quy thì chắn trên hai đường thẳng song song các cặp đoạn thẳng tỉ lệ.
Định lí Talet trong hình thang
Nếu một đường thẳng song song với hai đáy của hình thang và cắt hai cạnh bên thì nó định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.
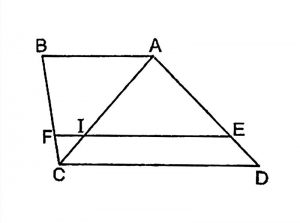
Cho hình thang ABCD, điểm E thuộc AD và F thuộc BC
Nếu EF // AB // CD, ta có AE/DE = BF/CF
Ngược lại, nếu: AE/DE = BF/CF à EF // AB// CD