Định nghĩa cấp số nhân, tổng cấp số nhân lùi vô hạn

Định nghĩa cấp số nhân

Cấp số nhân là một dãy số (hữu hạn hay vô hạn) mà trong đó, kể từ số hạng thứ hai, mỗi số hạng đều bằng tích của số hạng đứng ngay trước nó và một số q không đổi, nghĩa là: (un) là cấp số nhân ⇔ ∀n ⩾ 2, un = un−1.q
Số q được gọi là công bội của cấp số nhân

(tùy theo cách quy ước mà công bội được quy ước theo các chữ cái khác nhau có thể a,r..)

Như vậy, một cấp số nhân có dạng: u_n, u_nq, u_nq², u_nq³...

Tính chất cấp số nhân

Nếu (un) là một cấp số nhân thì kể từ số hạng thứ hai, bình phương của mỗi số hạng (trừ số hạng cuối đối với cấp số nhân hữu hạn) bằng tích của hai số hạng đứng kề nó trong dãy, tức là:

Cho dãy cấp số nhân: 2, 4, 8, 16..., ta có: 4²=2x8

           U_n=U₁.q^n-1

Nếu một cấp số nhân có số hạng đầu u₁ và công bội q≠0 thì số hạng tổng quát u_n của nó được xác định bởi công thức:

Số hạng tổng quát

Số hạng thứ n của cấp số nhân được tính bằng công thức

U_n=U.q^n-1 (trong đó n lớn hơn hoặc bằng 1)

Tổng n số hạng đầu tiên

S_n=u1 (qn-1)q-1

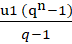
Tổng cấp số nhân lùi vô hạn: S_n=u1 1-q

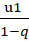
Lưu ý: Nếu công bội là:

Luyện tập:

1/ Cho cấp số nhân (un) có u3=24và u4=48. Hãy tính tổng 5 số hạng đầu tiên của cấp số đó.
Giải: Gọi q là công bội của cấp số nhân (un), ta có:  q=48/24=2
Do đó, theo định lí 2, ta được : 24=u3=u1.2². Suy ra u1=6. Vì thế, theo định lí 3, ta được S5=6.(1−2⁵)/(1−2)=186

2/ Một cấp số nhân có số hạng thứ nhất là 3 và công bội là 2.
a) Viết 6 số hạng đầu tiên.
b) Tính tổng của 6 số hạng đầu tiên.
c) Viết công thức tổng quát cho số hạng thứ n.
d) Tính tổng S của 100 số hạng đầu tiên.
Bài làm. a) 3, 6, 12, 24, 48, 96.
b) 3 + 6 + 12 + 24 + 48 + 96 = 189.
c) 3 × 2^(n - 1).
d) S = 3 + 6 + 12 +... + 3 × 2^99. 2S = 6 + 12 + 24 +... + 3 × 2^100. 2S - S = 3 × 2^100 - 3. Từ đó S = 3 × (2^100 - 1).

• Số dương: Các số hạng luôn có dấu cố định.
• Số âm: các số hạng là đan dấu giữa âm và dương..
• 0, mọi số hạng bằng 0.
• Lớn hơn 1, các số hạng tăng theo hàm mũ tới vô cực dương hoặc âm.
• 1, là một dãy không đổi.
• Giữa 1 và −1 nhưng khác không, chúng giảm theo hàm mũ về 0.
• −1, là một dãy đan dấu.
• Nhỏ hơn −1, chúng tăng theo hàm mũ về vô cực (dương và âm).