-
Câu Hỏi
1868
-
Thành Viên
799
-
Wiki-Hỏi-Đáp.Org
Wiki Hỏi đáp trực tuyến là website chia sẻ kiến thức cộng đồng về tất cả lĩnh vực từ giáo dục, kinh tế, xã hội khoa học, đời sống, gia đình...
Liên hệ tại: Wikihoidap.org@gmail.com
Liên kết hữu ích bạn nên xem: Alo789
-
Theo dõi Wiki Hỏi đáp
-
Bản quyền tại DMCA
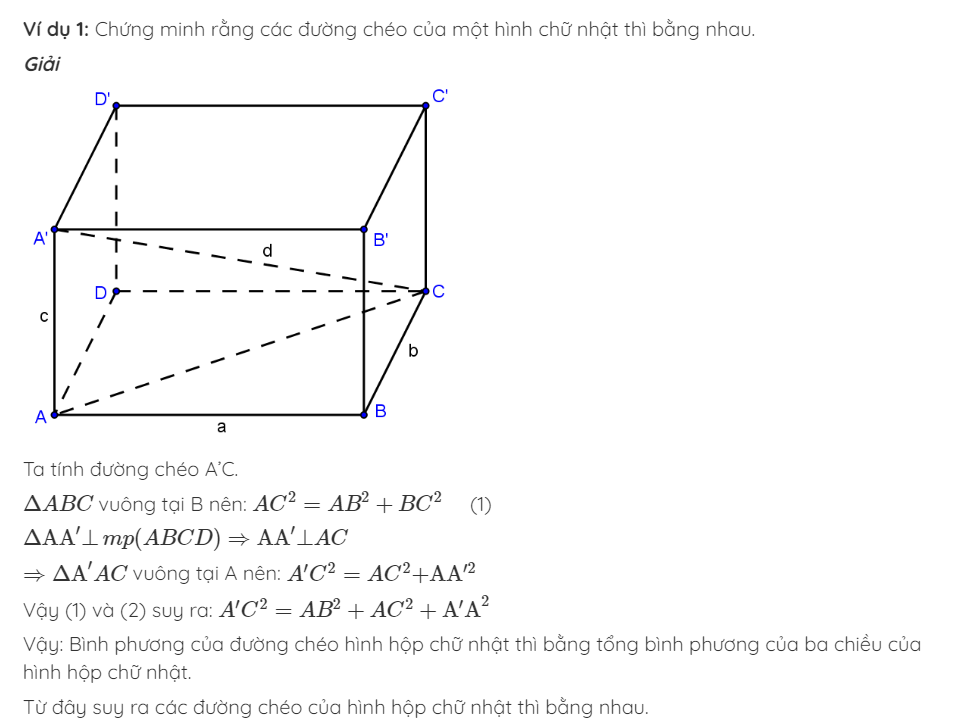
Hình lăng trụ đứng là gì? Cách tính Diện tích và Thể tích hình lăng trụ đứng
Hình lăng trụ đứng là gì? Đặc điểm nhận dạng ra sao? Cách tính diện tích, thể tích của hình lăng trụ bằng cách nào? Tất cả những thắc mắc đó sẽ được Wikihoidap.org giải đáp qua bài viết dưới đây!
Danh mục nội dung
Hình lăng trụ đứng là hình có:
- Hai đáy là hai đa giác phẳng bằng nhau và nằm trong hai mặt phẳng song song với nhau.
- Các cạnh bên thì vuông góc với các mặt phẳng chứa các đa giác đáy. Các mặt bên của lăng trụ đứng là các hình chữ nhật.
Các cạnh bên của lăng trụ đứng thì song song với nhau và bằng nhau, độ dài cạnh bên là chiều cao của lăng trụ đứng. Người ta gọi tên các hình lăng trụ theo tên của đa giác đáy: lăng trụ tam giác, lăng trụ tứ giác,… Hình lăng trụ đứng mà đáy là đa giác đều được gọi là lăng trụ đều.
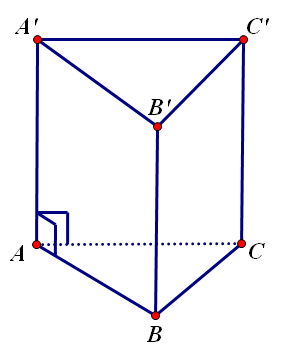
Tính chất của hình lăng trụ đứng
Trong chương trình toán học phổ thông, chúng ta đã được tiếp cận. Từ khái niệm của loại hình này, chúng ta có thể kết luận được những tính chất của nó.
- Là loại hình có các cạnh bên vuông góc với đáy
- Tất cả các mặt bên đều là hình chữ nhật
- Hình lăng trụ đứng có mặt phẳng chứa đáy là các mặt phẳng song song.
- Chiều cao của hình lăng trụ đứng là cạnh bên
Đây là hai tính chất quan trọng để phân biệt và nhận biết hình lăng trụ đứng với các hình lăng trụ khác. Những hình lăng trụ đứng có đáy là hình bình hành còn được biết tới với tên gọi là hình hộp đứng.
Công thức tính diện tích xung quanh và thể tích
Diện tích xung quanh hình lăng trụ đứng bằng tích chu vi đáy với chiều cao:
Sxq = 2.p.h (p: nửa chu vi đáy, h: chiều cao)
Diện tích toàn phần của hình lăng trụ đứng bằng tổng diện tích xung quanh với diện tích 2 đáy
Thể tích của hình lăng trụ đứng bằng tích của diện tích đáy và chiều cao
V = S.h (S: diện tích đáy, h: chiều cao)
Các dạng bài tập hình lăng trụ đứng
Dạng 1: Xác định mối quan hệ giữa cạnh, góc, mặt phẳng
Để giải dạng bài tập xác định mối quan hệ giữa cạnh, góc và mặt phẳng của hình lăng trụ đứng, ta cần áp dụng những tính chất của hình lăng trụ đứng. Đồng thời sử dụng những mối quan hệ song song hay vuông góc giữa các đường thẳng với đường thẳng, đường thẳng với mặt phẳng và mặt phẳng với mặt phẳng để giải thích và chứng minh.
Dạng 2: Tính độ dài, diện tích xung quanh, diện tích toàn phần, thể tích
Để giải dạng bài tập tính độ dài, diện tích xung quanh, diện tích toàn phần hay thể tích, ta cần áp dụng công thức tính diện tích xung quanh, diện tích toàn phần, thể tích…