Phương trình bậc 2 và nghiệm phương trình bậc hai đơn giản

Phương trình bậc hai là phương trình có dạng:

Ax² + bx + c = 0

với x là ẩn số chưa biết và a, b, c là các số đã biết sao cho a khác 0. Các số a, b, và c là những hệ số của phương trình và có thể phân biệt bằng cách gọi tương ứng hệ số bậc hai, hệ số bậc một, và hằng số hay số hạng tự do.

Vì phương trình bậc hai chỉ có một ẩn nên nó được gọi là phương trình "đơn biến". Phương trình bậc hai chỉ chứa lũy thừa của x là các số tự nhiên, bởi vậy chúng là một dạng phương trình đa thức, cụ thể là phương trình đa thức bậc hai do bậc cao nhất là hai.

Các cách giải phương trình bậc hai phổ biến là nhân tử hóa (phân tích thành nhân tử), phương pháp phần bù bình phương, sử dụng công thức nghiệm, hoặc đồ thị.

Cách giải phương trình bậc 2

Đặt Δ = b² − 4ac

• Nếu Δ < 0 thì phương trình vô nghiệm
• Nếu Δ = 0 thì phương trình có nghiệm kép x₁= x₂ = − b/2a
• Nếu Δ > 0 thì phương trình có hai nghiệm:

Định lý Vi-et về nghiệm của phương trình bậc 2

Định lý Vi-et thuận

Hai số x₁, x₂ là hai nghiệm của phương trình Ax² + bx + c = 0 khi và chỉ khi: 

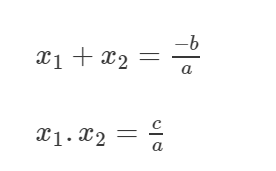
Định lý Vi-et đảo