-
Câu Hỏi
1868
-
Thành Viên
799
-
Wiki-Hỏi-Đáp.Org
Wiki Hỏi đáp trực tuyến là website chia sẻ kiến thức cộng đồng về tất cả lĩnh vực từ giáo dục, kinh tế, xã hội khoa học, đời sống, gia đình...
Liên hệ tại: Wikihoidap.org@gmail.com
Liên kết hữu ích bạn nên xem: Alo789
-
Theo dõi Wiki Hỏi đáp
-
Bản quyền tại DMCA
P-value là gì? Cách tính và ý nghĩa
P-value là gì? Ý nghĩa của P-value thế nào? Cách hiểu và tính toán của P-value. Cùng Wikihoidap tìm hiểu trong bài viết dưới đây nhé.
Danh mục nội dung
Giá trị xác suất của kiểm định: giá trị P ( P-value):
Chúng ta nhìn lại bài toán kiểm định 2 phía: H0: a= a0 ; H1: a ≠ a0 với trường hợp n ≥ 30 và chưa biết phương sai tổng thể. Giả sử mức ý nghĩa đang được xem xét là α1= 0,05 thì zα1=1,96 và miền bác bỏ tương ứng là Wα1 =(-¥; -1,96) È (1,96; +¥).
Nếu từ một mẫu cụ thể ta tính được zqsA = 2,0 Î Wα1 thì giả thiết H0 tương ứng bị bác bỏ. Giả thiết từ một mẫu cụ thể khác ta tính được zqsB = 10 chẳng hạn thì giả thiết H0 cũng bị bác bỏ. Ta nhận thấy việc bác bỏ H0 trong trường hợp mẫu sau có vẻ “thuyết phục” hơn.
Mặt khác, nếu thay đổi mức ý nghĩa đang được xem xét thành α2=0,02 thì zα2=2,33 và miền bác bỏ tương ứng là Wα2 =(-¥; -2,33) È (2,33; +¥). Lúc này ta vẫn bác bỏ H0 nếu zqsB= 10 nhưng lại phải chấp nhận H0 nếu dùng zqsA = 2,0.
Quá trình kiểm định như trên được gọi là kiểm định theo cách tiếp cận cổ điển. Bây giờ ta tìm hiểu một cách tiếp cận khác bài toán kiểm định. Thay vì kiểm định giả thiết với một mức ý nghĩa a định trước thì người ta cho rằng sau khi định rõ các giả thiết kiểm định H0 và giả thiết đối H1, ta thu thập các số liệu mẫu và xác định mức độ khẳng định việc bác bỏ giả thiết H0. Mức độ khẳng định này thường được gọi là giá trị xác suất P hay P-value.
Ta nói rằng mức ý nghĩa nhỏ nhất tại đó giả thiết H0 bị bác bỏ được gọi là giá trị P kết hợp với mẫu quan sát được. Người ta còn gọi giá trị P là mức ý nghĩa quan sát, nó cho biết xác suất mắc sai lầm loại I tối đa khi bác bỏ giả thiết Ho với một mẫu quan sát cụ thể.
Xét bài toán kiểm định trung bình tổng thể trong trường hợp mẫu lớn (n ³ 30) và chưa biết phương sai tổng thể. Tiêu chuẩn kiểm định là thống kê Z = (X-a0)√n/S nếu chấp nhận giả thiết H0 : “ a = a0” đúng.
- Giả thiết kiểm định H0 : “ a = a0”. H1: “a ¹ a0”.
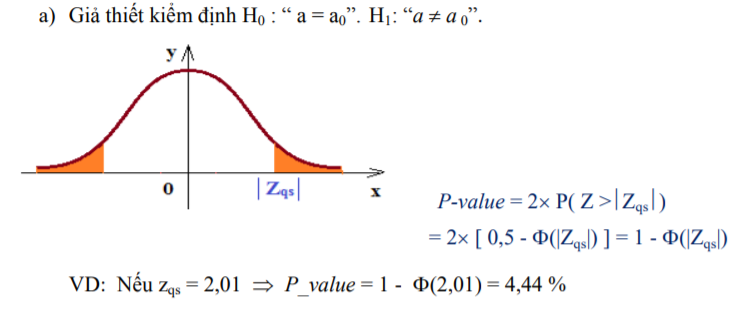
- Giả thiết kiểm định H0 : “ a = a0”. H1: “a < a0”.

- Giả thiết kiểm định H0 : “ a = a0”. H1: “a > a0”.
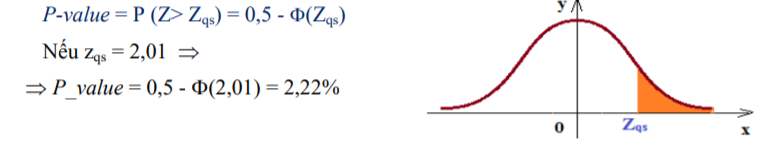
Trong VD ở mục a) P_value = 4,44% tức là giả thiết H0 sẽ bị bác bỏ khi mức ý nghĩa a được yêu cầu trong bài toán lớn hơn 4,44%. Nếu mức ý nghĩa a trong bài nhỏ hơn 4,44% thì ta phải công nhận giả thiết H0.
Các phần mềm thống kê hiện nay đều đưa ra P-value cho mỗi bài toán kiểm định để độc giả tự đánh giá kết quả. Ý tưởng chủ đạo là P-value càng nhỏ thì càng bác bỏ giả thiết mạnh, P-value càng lớn thì càng chấp nhận giả thiết mạnh.
Thông thường người ta tiến hành kiểm định theo nguyên tắc:
- Nếu 0,1 £ P-value: ta thường thừa nhận H0.
- Nếu 0,05 £ P-value < 0,1: cân nhắc cẩn thận trước khi bác bỏ H0.
- Nếu 0,01 £ P-value < 0,05: nghiêng về hướng bác bỏ H0 nhiều hơn.
- Nếu 0,001 £ P-value < 0,01: có thể ít băn khoăn khi bác bỏ H0.
- Nếu P-value < 0,001: có thể hoàn toàn yên tâm khi bác bỏ H0.
Trong các VD ở mục a) và c) ta tính được giá trị P tương đối nhỏ nên kết luận nghiêng về xu hướng bác bỏ H0. Còn VD ở mục b) khi zqs= -2,01 thì giá trị P quá lớn nên ta luôn chấp nhận H0.
Những trường hợp tiêu chuẩn kiểm định có các phân phối khác như phân phối Student, phân phối Khi bình phương, phân phối Fisher…, chúng ta có thể tìm giá trị P tương ứng với giá trị quan sát được lấy từ mẫu. Tuy nhiên do hạn chế của phần tra bảng nên chúng ta không trình bày.
Cách tính P-value trong kinh tế lượng
- Tính giá trị t khi biết độ tin cậy
- Lúc này, ta cần dùng cấu trúc hàm: = TINV (mức ý nghĩa alpha, tổng số quan sát N – 2)
- Xác định mức ý nghĩa alpha của giá trị thống kê t cho trước
- Dùng hàm: = TDIST (giá trị t, tổng số quan sát N – 2, số bên kiểm định).
- Tính giá trị f khi biết độ tin cậy
- Sử dụng cấu trúc hàm: = FINV (mức ý nghĩa alpha, số biến giải thích hoặc số ràng buộc, tổng số quan sát – số tham số).
- Xác định mức ý nghĩa alpha của giá trị thống kê f cho trước:
- Dùng cấu trúc hàm: = FDIST (giá trị f, số biến giải thích hoặc số ràng buộc, tổng số quan sát – số tham số).
- Với số biến giải thích = K1, số ràng buộc = J. Tổng số quan sát trừ số tham số = N-K.



